My Haskell Tiny Game Jam Submissions: Othello & Lol
This post is a last-minute write-up for my participation in the Haskell Tiny Game Jam. The goal was to implement a game that fits into 10 lines of 80 characters. I have submitted two entries: one is a mini-othello game, the other is a meta game called "lol".
Mini Othello
It is a minimum Othello game implementation with MiniMax "AI" opponent using GHC 9.X with only the "prelude" module allowed.
The rule of the game is: "There are sixty-four identical game pieces called disks, which are light on one side and dark on the other. Players take turns placing disks on the board with their assigned color facing up. During a play, any disks of the opponent's color that are in a straight line and bounded by the disk just placed and another disk of the current player's color are turned over to the current player's color. The objective of the game is to have the majority of disks turned to display one's color when the last playable empty square is filled." (https://en.wikipedia.org/wiki/Reversi)
To play the game, checkout the tiny game repository and type ./play mini-othello:

I implemented the game entirely in minified code, so the variable and function names will be pretty cryptic!
Functions Overview
First, I represent the game state with a product type of Board and Side (only conceptually, but without actual code):
type Side = Black | White | None type Coordinate = (Int, Int) -- from (0,0) to (7,7) type Board = [Char] -- 64 of them! -- | Game state type alias type GameState = (Board, Side) n = "_XO" -- visually they are reprensed these chars.
Then I implemented a helper function v for checking the number of flips per each line. There are 8 different
directions the line can go, they are all enumerable by a StepCoordinate type.
-- number of steps (-1,0 or 1) in each direction to represent 8 different directions. type StepCoordinate = (Int, Int) -- | Check number of flips for one single direction v :: GameState -> (GameState, Int) -> Coordinate -> StepCoordinate -> State -> (GameState, Int) v savedGameState (currentGameState, nFlips) cor stepCor state -> (newGameState, nFlips)
Then the % operator for trial plays. Because this is used so often, the usage of this binary operator saves a lot of
spaces!
(%) :: GameState -> Coordinate -> (GameState, Int) (%) inGameState -> cor -> (outGameState, nFlips)
The q function moves the game state to the next round.
-- | Play and move to next round q :: GameState -> Coordinate -> GameState q currentGameState -> cor -> nextRoundGameState
The z function starts the game in the IO monad.
-- | Start game z :: Side -> GameState -> IO () z humanSide (initialBoard,currentSide)
The e function is the game strategy for the AI:
-- | Strategy function! e :: GameState -> GameState
It should use the q function to move the game state forward.
There are three game strategies attempted during the code jam:
- A naive strategy that finds the first possible move.
- A greedy strategy that finds the immediate move that flips the most pieces.
- A MiniMax strategy that tries to play the game with a few levels of depth with MiniMax decision rules.
I will enlist the code of (3) here. And because of its minified nature, it looks pretty hideous, I admit:
g h a=f(\c e->i e>i c?e$c)(-65*h,(0,0))$ (\((b,p),d)->(h*(h*p==0?j a`c`i b$i$g(div h(-2))b),d))& (((,)=<<(a%))&k r); e a=q a.j$g 4a
Here g 4a is a recursive function starting with 4, and it oscillates between positive ("max" stage) and negative
("min" stage) and halves at the same time (g -2a, then g 0a). This is a trick to use a single number to represent
the stage and depth limit of the minimax process.
The evaluation function is kept simple; the more flips, the better. In a better strategy, certain pieces are worth more (at the corner or at the side).
Code Golfing Tricks
Compact Ternary Operator (Prelude)
If you use a lot of if then else, use this test?yes$no to save a lot of spaces:
infixr 1?;(b?x)y|b=x|0<3=y;
If you are not limited to using only "prelude" module, you might also use bool :: a -> a -> Bool -> a in base.
Shortest Function for "Other Side"
o=1:2:o, so that o 1=2 and o 2=1. Any other output is uninteresting!
This is a funny function enabled by Haskell's lazy evaluation semantics.
Shortest Cross Product Function
k=(<*>)=<<((,)<$>), so that:
k[-1..1]is for interacting through all 8 directions ([1,1],[1,0],[1,-1],[0,1],[0,-1][-1,-1],[-1,1],[-1,0]), the 9th direction[0,0]is uninteresting and doesn't create trouble fur us.k[0..7]generates all 64 positions on the board for iterating through them.
The alternative would be using twice List applicative; this version saves spaces!
Make a move
This bizarre ternary function put a piece "w" at position "i" on the board "b":
(w^i)b=take i b++w:drop (i+1)b;
Other Ad-hoc One-Letter Functions
More tips about minifying and unminifying techniques can be found at: https://github.com/haskell-game/tiny-games-hs/issues/52
Lol - The Meta Game
My second submission to the game jam is less serious. In fact, it is a knock-off of the lolcat program! But it is tightly integrated with the game itself, hence a meta game!
The idea of it is straightforward: it pipes the "play" command to colorize its output and add additional text effects depending on how many "lols" you have inserted in the command line, e.g.:
./play lol lol lol lol lol ski would give you a rather trippy ski trip:
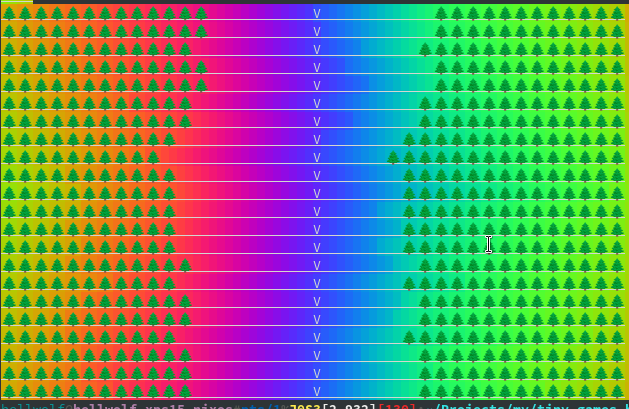
The trick of using the applicative list to generate an infinite list of variations:
(,,)<$>[1..]<*>s[38,48]<*>s[0,4,5]
The first parameter is the frequency of the rainbow color effects; the second one is the anis-terminal color code choice for foreground or background; the third one is additional text effects such as underlined texts and blinking texts.
Conclusion
I have enjoyed the journey, learned and jammed with various Haskell syntaxes for code golfing. Comparing to perl golf in the old days, code golfing in Haskell is a joy: if it type-checks, it usually works!
And I would like to thank the organizers, the participants, and all the fine folks at #haskell-game.



