Posts tagged "category-theory":
PatternMatchable, Yoneda Embedding, and Adjunction
Pattern Matching For an Embedded DSL
For a embedded DSL m :: Type -> Type, we would like to introduce a function match to match a pattern and a function
be to construct such a pattern. Here is an example of using them:
-- Note: BlockArguments & LambdaCase extensions used -- Pattern match @pat@ of two cases, and recreate the pattern @pat'@ pat' = match pat \case Maybe a -> be (Maybe a) Nothing -> be Nothing
Generally, the property of pattern matchable is \pat -> match pat be ≃ id.
How about their type signatures? Let's have the pattern as pat :: m p, the pattern cases c, and the pattern matching
result as :: m b. Then we have:
match :: ∀ m p c b. m p -> (c -> m b) -> m b be :: ∀ m p c. c -> m p
However, typically, in any language, b should be constrained, say by k. Now, we need a type class to put everything
together:
class PatternMatchable m k p c | m -> k, m p -> c, c -> m p where match :: ∀ b. k b => m p -> (c -> m b) -> m b be :: ∀ . c -> m p
Indeed, this is the code used in the Yolc project. As a further illustration, here is a couple of example instances of
the PatternMatchable from the Yolc project:
-- Pattern matching of Maybe values instance PatternMatchable (YulCat eff r) YulCatObj (Maybe (INTx s n)) (Maybe (YulCat eff r (INTx s n))) -- Pattern matching of Solo tuple instance PatternMatchable (YulCat eff r) YulCatObj (Solo a) (YulCat eff r a) -- Pattern matching of tuple PatternMatchable (YulCat eff r) YulCatObj (a1, a2) (YulCat eff r a1, YulCat eff r a2)
Working Backward: Yoneda Embedding
How can you come up with such a design in the first place?
While admittedly, I had to look at the problem for a very long time with trial and error on paper or in code, eventually, the solution came to mind like a light bulb lit up.
More experienced practitioners may find this task easy. But the question is, apart from practicing Haskell or functional programming more, what sort of general knowledge should one learn to find these solutions faster?
I went back to category theory for answers, and indeed, it is an application of no other than the Yoneda lemma itself. Specifically, it is the special case "Yoneda embedding."
Bartosz Milewski has a wonderful article about Yoneda Embedding itself, I will not repeat here. Instead, I take its conclusion directly below.
In its categorical formulation, in the functor category [C, Set], a natural transformation from hom-functor C(a, -)
to hom-functor C(b, -) is isomorphic to C(b, a).
[C, Set](C(a, -), C(b, -)) ≃ C(b, a)
We can translate the above to its equivalent Haskell code.
∀ x. (a -> x) -> (b -> x) ≃ b -> a
Now, let's work backward. We should be able to implement be :: c -> m p easily for the DSL. However, it is not possible
for its inverse: not_possible :: m p -> c. This is because c is not part of the language m, so it cannot "escape"
as an independent value.
At this point, you may use some ad-hoc functional programming jargon, such as "continuation," to find the match
function solution. Instead, I'd like to show that with Yoneda embedding, it becomes a rather mechanical exercise. Here
is how:
- Since we cannot implement
m p -> c, we apply Yoneda embedding. - We then have
m p -> c ≃ (c -> x) -> (m p -> x). - We replace
xwithm b, the result we are looking for:(c -> m b) -> (m p -> m b). - We remove the second pair of brackets, which are redundant:
(c -> m b) -> m p -> m b. - We flip the first and second argument:
m p -> (c -> m b) -> m b. - We arrived at the same signature of the
matchfunction.
As the category theory often promises, every knowledge we know of is likely an example of a category and some universal properties. I am glad I have found an application of Yoneda lemma after all.
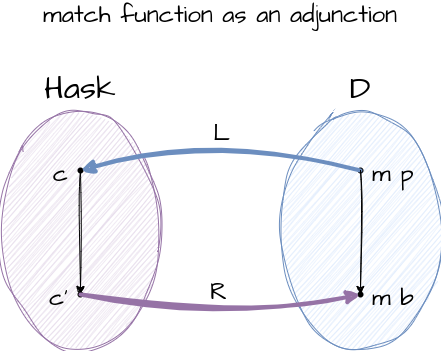
Adjunction Between Hask and Your DSL
Here is another observation of how match function is also an adjunction.
Again, I will refer you to Bartosz' article about adjunctions, for more about the topic.
Let's say your eDSL program m a is of category D. Additionally, we can also view Haskell types as objects in the category of
Hask. Technically, as an deep embedded DSL, all objects in D is also in Hask. However, as a DSL, there should be no
morphism from object in D to ones outside of D. For this reason, we illustrate the match function as an
adjunction that depicts D and Hask not overlapped for better visuals.
Conclusion
There is one thing about Category Theory that I have found other such as @ChShersh also agree with "you can program perfectly fine without it. Many people do, it's not the end of the world. But it's not a great life either."
In a world where AI can increasingly spit out code patterns that accomplish tasks effectively, I would like to believe that category theory and mathematics are what give meaning to our lives by training our brains with these beautiful and elegant knowledge.



